Facebook 天数字符串预估演算法 Prophet 的科学研究

Prophet 概要

Facebook 今年开放源码了两个天数字符串预估的演算法，叫作 fbprophet，它的非官方邮箱与基本如是说源自于下列几个中文网站：

从官方中文网站的如是说上看，Facebook 所提供更多的 prophet 演算法不仅能处置天数字符串存在一些极度值的情况，也能处置部分缺位值的情况，还能几乎半自动地预估天数字符串今后的市场走势。从学术论文上的叙述上看，那个 prophet 演算法是如前所述天数字符串降解和机器学习的插值来做的，当中在插值数学模型的时候采用了 pyStan 那个开源辅助工具，因而能在较快的天数内获得须要预估的结论。除此以外，为了方便快捷逻辑学家，机器学习专业人士等群体的采用，prophet 同时提供更多了 R 词汇和 Python 词汇的USB。从总体的如是说上看，如果是一般来说的商业性分析或是数据挖掘的市场需求，都能试著采用那个开放源码演算法来预估今后天数字符串的市场走势。

Prophet 的演算法基本原理

Prophet 数据的输入和输入

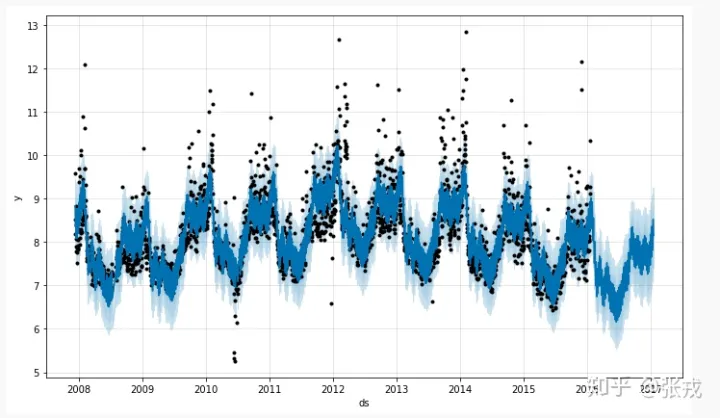
具体来说让我们上看两个常用的天数字符串情景，白色则表示原初的天数字符串对数点，浅蓝色的线则表示采用天数字符串来插值所获得的值域，而浅蓝色的线则表示天数字符串的两个概率密度函数，也是简而言之的科学合理的原函数和上界。prophet 所做的事情是：

就一般来说情况来说，天数字符串的app储存文件格式为天数戳和值这种文件格式，更多的话能提供更多天数字符串的 ID，条码等文本。因而，app储存的天数字符串一般来说都是下列的形式。当中 date 指的是具体文本的天数戳，category 指的是wlzwyyan某一的天数字符串 id，value 指的是在 date 下那个 category 天数字符串的值域，label 指的是育苗记号的条码（0 则表示极度，1‘ 则表示恒定，unknown 则表示没有记号或是育苗推论不清）。

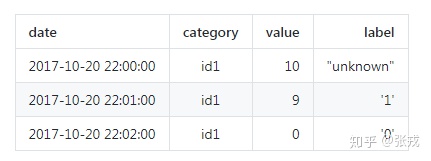
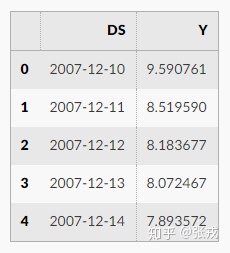
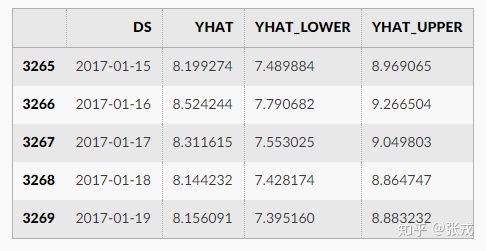
而 fbprophet 所须要的天数字符串也是这种文件格式的，根据官方中文网站的叙述，只要用 csv 文件储存两列即可，第一列的英文名字是 ds, 第二列的名称是 y。第一列则表示天数字符串的天数戳，第二列则表示天数字符串的值域。通过 prophet 的计算，能计算出 yhat，yhat_lower，yhat_upper，分别则表示天数字符串的预估值，预估值的上界，预估值的原函数。两份表格如下面的两幅图则表示。

Prophet 的演算法实现

在天数字符串分析领域，有一种常用的分析方法叫作天数字符串的降解（Decomposition of Time Series），它把天数字符串yt y_{t} 分成几个部分，分别是季节项 StS_{t} ，趋势项 TtT_{t} ，剩余项 RtR_{t} 。也是说对所有的 t≥0 t\geq 0 ，都有

yt=St+Tt+Rt.y_{t} = S_{t} + T_{t} + R_{t}.

除了加法的形式，还有乘法的形式，也是：

yt=St×Tt×Rt.y_{t} = S_{t} \times T_{t} \times R_{t}.

以上式子等价于 ln⁡yt=ln⁡St+ln⁡Tt+ln⁡Rt\ln y_{t} = \ln S_{t} + \ln T_{t} + \ln R_{t} 。所以，有的时候在预估数学模型的时候，会先取对数，然后再进行天数字符串的降解，就能获得乘法的形式。在 fbprophet 演算法中，作者们如前所述这种方法进行了必要性的改进和优化。

一般来说来说，在实际生活和生产环节中，除了季节项，趋势项，剩余项之外，一般来说还有节假日的效应。所以，在 prophet 演算法里面，作者同时考虑了以上四项，也是：

y(t)=g(t)+s(t)+h(t)+ϵt.y(t) = g(t) + s(t) + h(t) + \epsilon_{t}.

当中 g(t)g(t) 则表示趋势项，它则表示天数字符串在非周期上面的变化趋势； s(t)s(t) 则表示周期项，或是称为季节项，一般来说来说是以周或是年为单位； h(t)h(t)表示节假日项，则表示在当天是否存在节假日；ϵt\epsilon_{t} 则表示误差项或是称为剩余项。Prophet 演算法是通过插值这几项，然后最后把它们累加起来就获得了天数字符串的预估值。

趋势项数学模型 g(t)g(t)

在 Prophet 演算法里面，趋势项有两个重要的函数，两个是如前所述逻辑回归函数（logistic function）的，另两个是如前所述分段线性函数（piecewise linear function）的。

具体来说，我们来如是说一下如前所述逻辑回归的趋势项是怎么做的。

如果回顾逻辑回归函数的话，一般来说都会想起这样的形式： σ(x)=1/(1+e−x),\sigma(x) = 1/(1+e^{-x}), 它的导数是 σ′(x)=σ(x)⋅(1−σ(x)),\sigma(x) = \sigma(x) \cdot(1-\sigma(x)), 并且 limx→+∞σ(x)=1,\lim_{x\rightarrow +\infty} \sigma(x) = 1, limx→−∞σ(x)=0.\lim_{x\rightarrow -\infty} \sigma(x) = 0. 如果增加一些参数的话，那么逻辑回归就能改写成：

f(x)=C/(1+e−k(x−m)),f(x) = C / (1 + e^{-k(x-m)}),

这里的 CC 称为抛物线的最大渐近值， kk 则表示抛物线的增长率， mm 则表示抛物线的中点。当 C=1,k=1,m=0C=1, k = 1, m =0 时，恰好是大家常用的 sigmoid 函数的形式。从 sigmoid 的函数表达式上看，它满足下列的微分方程： y′=y(1−y)y=y(1-y) 。

那么，如果采用分离变量法来求解微分方程 y′=y(1−y)y=y(1-y) 就能获得：

y′y+y′1−y=1⇒ln⁡y1−y=1⇒y=1/(1+Ke−x).\frac{y}{y} + \frac{y}{1-y} = 1 \Rightarrow \ln\frac{y}{1-y} = 1 \Rightarrow y = 1/(1+K e^{-x}).

但是在现实环境中，函数 f(x)=C/(1+e−k(x−m)) f(x) = C / (1+e^{-k(x-m)}) 的三个参数 C,k,mC, k, m不可能都是常数，而很有可能是随着天数的迁移而变化的，因而，在 Prophet 里面，作者考虑把这三个参数全部换成了随着天数而变化的函数，也是C=C(t),k=k(t),m=m(t).C = C(t), k = k(t), m = m(t).

除此以外，在现实的天数字符串中，抛物线的市场走势肯定不会一直保持不变，在某些某一的时候或是有着某种潜在的周期抛物线会发生变化，这种时候，就有学者会去科学研究变点检测，也是简而言之 change point detection。例如下面的这幅图的 t1∗,t2∗t_{1}^{*}, t_{2}^{*}是天数字符串的两个变点。

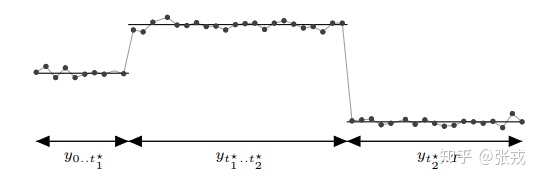
在 Prophet 里面，是须要设置变点的位置的，而每一段的趋势和市场走势也是会根据变点的情况而改变的。在程序里面有两种方法，一种是通过育苗指定的方式指定变点的位置；另外一种是通过演算法源自动选择。在默认的函数里面，Prophet 会选择 n_changepoints = 25 个变点，然后设置变点的范围是前 80%（changepoint_range），也是在天数字符串的前 80% 的区间内会设置变点。通过 forecaster.py 里面的 set_changepoints 函数能知道，具体来说要看一些边界条件是否科学合理，例如天数字符串的点数是否少于 n_changepoints 等文本；其次如果边界条件符合，那变点的位置是均匀分布的，这一点能通过 np.linspace 那个函数看出来。

下面假设已经放置了 SS 个变点了，并且变点的位置是在天数戳 sj,1≤j≤Ss_{j}, 1\leq j\leq S 上，那么在这些天数戳上，我们就须要给出增长率的变化，也是在天数戳 sjs_{j} 上发生的 change in rate。能假设有这样两个向量： δ∈RS,\boldsymbol{\delta}\in\mathbb{R}^{S}, 当中 δj\delta_{j} 则表示在天数戳 sjs_{j} 上的增长率的变化量。如果一开始的增长率我们采用 kk 来代替的话，那么在天数戳 tt 上的增长率是 s_{j}} \delta_{j}">k+∑j:t>sjδjk + \sum_{j:t>s_{j}} \delta_{j} ，通过两个指示函数 a(t)∈{0,1}S\mathbf{a}(t)\in \{0,1\}^{S} 是

aj(t)={1, if t≥sj,0, otherwise.a_{j}(t) = \begin{cases} 1, \text{ if } t\geq s_{j},\\ 0, \text{ otherwise.} \end{cases}

那么在天数戳 t t 上面的增长率是 k+aTδ.k + \mathbf{a}^{T}\boldsymbol{\delta}. 一旦变化量 kk 确定了，另外两个参数 mm 也要随之确定。在这里须要把线段的边界处置好，因而通过数学计算能获得：

因而，如前所述分段线性函数的数学模型形如：

g(t)=(k+a(t)δ)⋅t+(m+a(t)Tγ),g(t)=(k+\boldsymbol{a}(t)\boldsymbol{\delta})\cdot t+(m+\boldsymbol{a}(t)^{T}\boldsymbol{\gamma}),

当中 k k 则表示增长率（growth rate）， δ \boldsymbol{\delta} 则表示增长率的变化量， mm则表示 offset parameter。而这两种方法（分段线性函数与逻辑回归函数）最大的区别是γ\boldsymbol{\gamma} 的设置不一样，在分段线性函数中， γ=(γ1,⋯,γS)T,\boldsymbol{\gamma}=(\gamma_{1},\cdots,\gamma_{S})^{T}, γj=−sjδj.\gamma_{j}=-s_{j}\delta_{j}. 注意：这与之前逻辑回归函数中的设置是不一样的。

在 Prophet 的源代码中，forecast.py 那个函数里面包含了最关键的步骤，当中 piecewise_logistic 函数则表示了前面所说的如前所述逻辑回归的增长函数，它的输入包含了 cap 那个分项，因而须要用户事先指定 capacity。而在 piecewise_linear 那个函数中，是不须要 capacity 那个分项的，因而 m = Prophet() 那个函数默认的采用 growth = linear 那个增长函数，也能写作 m = Prophet(growth = linear)；如果想用 growth = logistic，就要这样写：

变点的选择（Changepoint Selection）

在如是说变点之前，先要如是说一下 Laplace 分布，它的概率密度函数为：

f(x|μ,b)=exp⁡(−|x−μ|/b)/2b, f(x|\mu, b) = \exp\bigg(-|x-\mu|/b\bigg)/2b,

当中 μ\mu 则表示位置参数， 0">b>0 b>0 则表示尺度参数。Laplace 分布与正态分布有一定的差异。

在 Prophet 演算法中，是须要给出变点的位置，个数，以及增长的变化率的。因而，有三个比较重要的分项，那是

changepoint_range 指的是百分比，须要在前 changepoint_range 那么长的天数序列中设置变点，在默认的函数中是 changepoint_range = 0.8。n_changepoint 则表示变点的个数，在默认的函数中是 n_changepoint = 25。changepoint_prior_scale 则表示变点增长率的分布情况，在学术论文中，δj∼Laplace(0,τ) \delta_{j} \sim Laplace(0,\tau) ，这里的 τ\tau是 change_point_scale。

在整个开放源码框架里面，在默认的情景下，变点的选择是如前所述天数字符串的前 80% 的历史数据，然后通过等分的方法找到 25 个变点（change points），而变点的增长率是满足 Laplace 分布 δj∼Laplace(0,0.05)\delta_{j} \sim Laplace (0,0.05) 的。因而，当 τ\tau 趋近于零的时候， δj \delta_{j}也是趋向于零的，此时的增长函数将变成全段的逻辑回归函数或是线性函数。这一点从g(t)g(t) 的定义能轻易地看出。

对今后的预估（Trend Forecast Uncertainty）

从历史上宽度为 TT 的数据中，我们能选择出 SS 个变点，它们所对应的增长率的变化量是 δj∼Laplace(0,τ) \delta_{j} \sim Laplace(0,\tau)。此时我们须要预估今后，因而也须要设置适当的变点的位置，从代码中看，在 forecaster.py 的 sample_predictive_trend 函数中，通过 Poisson 分布等概率分布方法找到新增的 changepoint_ts_new 的位置，然后与 changepoint_t 拼接在一起就获得了整段字符串的 changepoint_ts。

第一行代码的 1 保证了 changepoint_ts_new 里面的元素都大于 change_ts 里面的元素。除了变点的位置之外，也须要考虑 δ\delta 的情况。这里令 λ=∑j=1S|δj|/S\lambda = \sum_{j=1}^{S}|\delta_{j}|/S ，于是新的增长率的变化量是按照下面的规则来选择的：当 T">j>T j>T 时，

δj={0, with probability (T−S)/T∼Laplace(0,λ), with probability S/T.\delta_{j}=\begin{cases} 0 \text{, with probability } (T-S)/T \\ \sim Laplace(0,\lambda) \text{, with probability } S/T \end{cases}.

季节性趋势

几乎所有的天数字符串预估数学模型都会考虑那个因素，因为天数字符串一般来说会随着天，周，月，年等季节性的变化而呈现季节性的变化，也称为周期性的变化。对于周期函数来说，大家能马上联想到的是正弦余弦函数。而在数学分析中，区间内的周期性函数是能通过正弦和余弦的函数来则表示的：假设 f(x) f(x) 是以 2π2\pi 为周期的函数，那么它的傅立叶级数是 a0+∑n=1∞(ancos⁡(nx)+bnsin⁡(nx))a_{0} + \sum_{n=1}^{\infty}(a_{n}\cos(nx) + b_{n}\sin(nx)) 。

在学术论文中，作者采用傅立叶级数来模拟天数字符串的周期性。假设 PP 则表示天数字符串的周期， P=365.25P = 365.25 则表示以年为周期， P=7P = 7则表示以周为周期。它的傅立叶级数的形式都是：

s(t)=∑n=1N(ancos⁡(2πntP)+bnsin⁡(2πntP)).s(t) = \sum_{n=1}^{N}\bigg( a_{n}\cos\bigg(\frac{2\pi n t}{P}\bigg) + b_{n}\sin\bigg(\frac{2\pi n t}{P}\bigg)\bigg).

就作者的经验来说，对于以年为周期的字符串（ P=365.25P = 365.25 ）来说， N=10N = 10 ；对于以周为周期的字符串（P=7P = 7 ）来说， N=3N = 3 。这里的参数能形成列向量：

β=(a1,b1,⋯,aN,bN)T.\boldsymbol{\beta} = (a_{1},b_{1},\cdots,a_{N},b_{N})^{T}.

当 N=10N = 10 时，

X(t)=[cos⁡(2π(1)t365.25),⋯,sin⁡(2π(10)t365.25)]X(t) = \bigg[\cos\bigg(\frac{2\pi(1)t}{365.25}\bigg),\cdots,\sin\bigg(\frac{2\pi(10)t}{365.25}\bigg)\bigg]

当 N=3N = 3 时，

X(t)=[cos⁡(2π(1)t7),⋯,sin⁡(2π(3)t7)].X(t) = \bigg[\cos\bigg(\frac{2\pi(1)t}{7}\bigg),\cdots,\sin\bigg(\frac{2\pi(3)t}{7}\bigg)\bigg].

因而，天数字符串的季节项是： s(t)=X(t)β,s(t) = X(t) \boldsymbol{\beta}, 而 β\boldsymbol{\beta} 的初始化是 β∼Normal(0,σ2)\boldsymbol{\beta} \sim Normal(0,\sigma^{2})。这里的σ\sigma 是通过 seasonality_prior_scale 来控制的，也是说 σ=\sigma= seasonality_prior_scale。那个值越大，则表示季节的效应越明显；那个值越小，则表示季节的效应越不明显。同时，在代码里面，seasonality_mode 也对应着两种模式，分别是加法和乘法，默认是加法的形式。在开放源码代码中， X(t)X(t)函数是通过 fourier_series 来构建的。

节假日效应（holidays and events）

在现实环境中，除了周末，同样有很多节假日，而且不同的国家有着不同的假期。在 Prophet 里面，通过维基百科里面对各个国家的节假日的叙述，hdays.py 收集了各个国家的特殊节假日。除了节假日之外，用户还能根据自身的情况来设置必要性的假期，例如 The Super Bowl，双十一等。

由于每个节假日对天数字符串的影响程度不一样，例如春节，国庆节则是七天的假期，对于劳动节等假期来说则假日较短。因而，不同的节假日能看成相互独立的数学模型，并且能为不同的节假日设置不同的前后窗口值，则表示该节假日会影响前后一段天数的天数字符串。用数学词汇来说，对与第ii 个节假日来说， DiD_{i} 则表示该节假日的前后一段天数。为了则表示节假日效应，我们须要两个适当的指示函数（indicator function），同时须要两个参数 κi\kappa_{i}来则表示节假日的影响范围。假设我们有LL 个节假日，那么

h(t)=Z(t)κ=∑i=1Lκi⋅1{t∈Di},h(t)=Z(t) \boldsymbol{\kappa}=\sum_{i=1}^{L} \kappa_{i}\cdot 1_{\{t\in D_{i}\}},

当中 Z(t)=(1{t∈D1},⋯,1{t∈DL}),κ=(κ1,⋯,κL)T.Z(t)=(1_{\{t\in D_{1}\}},\cdots,1_{\{t\in D_{L}\}}), \text{ } \boldsymbol{\kappa}=(\kappa_{1},\cdots,\kappa_{L})^{T}.

当中 κ∼Normal(0,v2)\boldsymbol{\kappa}\sim Normal(0,v^{2}) 并且该正态分布是受到 v=v =holidays_prior_scale 那个分项影响的。默认值是 10，当值越大时，则表示节假日对数学模型的影响越大；当值越小时，则表示节假日对数学模型的效果越小。用户能根据自己的情况自行调整。

数学模型插值（Model Fitting）

按照以上的解释，我们的天数字符串已经能通过增长项，季节项，节假日项来构建了，i.e.

y(t)=g(t)+s(t)+h(t)+ϵy(t)=g(t)+s(t)+h(t)+\epsilon

下一步我们只须要插值函数就能了，在 Prophet 里面，作者采用了 pyStan 那个开放源码辅助工具中的 L-BFGS 方法来进行函数的插值。具体文本能参考 forecast.py 里面的 stan_init 函数。

Prophet 中能设置的参数

在 Prophet 中，用户一般来说能设置下列四种参数：

如果不想设置的话，采用 Prophet 默认的参数即可。

Prophet 的实际采用

Prophet 的简单采用

因为 Prophet 所须要的两列名称是 ds 和 y，当中，ds 则表示天数戳，y 则表示天数字符串的值，因而一般来说来说都须要修改 pd.dataframe 的列英文名字。如果原来的两列英文名字是 timestamp 和 value 的话，只须要这样写：

如果 timestamp 是采用 unixtime 来记录的，须要修改成 YYYY-MM-DD hh:mm:ss 的形式：

在一般来说情况下，天数字符串须要进行归一化的操作，而 pd.dataframe 的归一化操作也十分简单：

然后就能初始化数学模型，然后插值数学模型，并且进行天数字符串的预估了。

而 freq 指的是 pd.dataframe 里面的两个分项，min 则表示按分钟来收集的天数字符串。具体文本参见文档：http://pandas.pydata.org/pandas-docs/stable/timeseries.html#offset-aliases

在进行了预估操作之后，一般来说都希望把时间字符串的预估趋势画出来：

如果要画出更详细的分项，例如中间线，上上界，那么能这样写：

其实 Prophet 预估的结论都放在了变量 forecast 里面，打印结论的话能这样写：第一行是打印所有天数戳的预估结论，第二行是打印最后五个天数戳的预估结论。

Prophet 的参数设置

Prophet 的默认参数能在 forecaster.py 中看到：

增长函数的设置

在 Prophet 里面，有两个增长函数，分别是分段线性函数（linear）和逻辑回归函数（logistic）。而 m = Prophet() 默认采用的是分段线性函数（linear），并且如果要是用逻辑回归函数的时候，须要设置 capacity 的值，i.e. df[cap] = 100，否则会出错。

变点的设置

在 Prophet 里面，变点默认的选择方法是前 80% 的点中等距选择 25 个点作为变点，也能通过下列方法源自行设置变点，甚至能人为设置某些点。

而变点的作图能采用：

周期性的设置

一般来说来说，能在 Prophet 里面设置周期性，无论是按月还是周其实都是能设置的，例如：

节假日的设置

有的时候，由于双十一或是一些特殊节假日，我们能设置某些天数是节假日，并且设置它的前后影响范围，也是 lower_window 和 upper_window。

结束语

对于商业性分析等领域的天数字符串，Prophet 能进行很好的插值和预估，但是对于一些周期性或是趋势性不是很强的天数字符串，用 Prophet 可能就不合适了。但是，Prophet 提供更多了一种时序预估的方法，在用户不是很懂天数序列的前提下都能采用那个辅助工具获得两个能接受的结论。具体文本是否用 Prophet 则须要根据具体文本的天数字符串来确定。

参考文献：