一文入门Facebook开源向量检索框架Faiss（如何开facebook）_facebook知识

向量相似度索引，即依照两个向量Q从海量统计数据的向量复本寻找TopK个与Q最相似或是距最近的向量，其在工业中有着广泛的应用情景，比如影像索引、文档语法索引以及推荐系统中如前所述User与Item的Embedding向量停售等。在制造环境中，被搜寻的向量库往往是海量统计数据，甚至超过了缓存的管制，而且面临着高mammalian与低延后的需求。Facebook开放源码了两个ANN向量相似度索引架构Faiss，为我们较好的解决了那个问题，它提供更多了多种演算法与距测度形式，全力支持GPU快速并且提供更多了C++与Python API。责任编辑将结合其全力支持的演算法对其采用形式做个简单的介绍。

基本上演算法

为的是快速向量索引的过程，问世了许多演算法，在采用Faiss或是其他向量索引架构前需要对那些演算法有两个基本上的了解。

Brute-force搜寻

从整个向量库里面HMPP搜寻，计算维数与向量库大小成差值。

ANN搜寻

Brute-force搜寻的效率太低，为的是大力推进搜寻的速度，制造实践中问世了近似于搜寻形式——ANN(Approximate Nearest Neighbor)。几乎所有的ANN形式都是将搜寻的拆分成许多的子内部空间，在搜寻的时候，通过某种形式快速将搜寻覆盖范围管制在二个子内部空间，接着在那些子内部空间里做Brute-force搜寻。

目前比较的ANN实现形式主要有四种：如前所述树的形式、基元形式、向量定量形式。

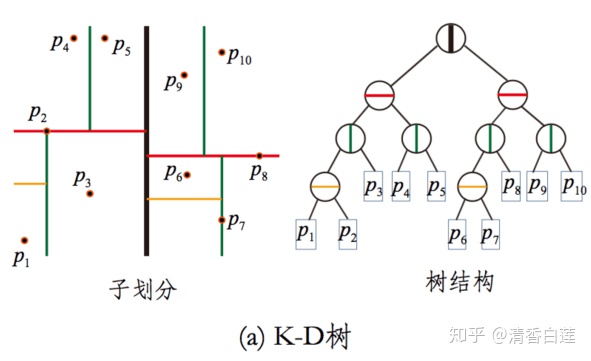
如前所述树的形式：根结点代表HMPP的统计数据，子结点相当于对父结点的内部空间拆分，叶结点是最轻的子内部空间。最常见的是KD树，其内部空间拆分的形式是选择标准差最大的方向展开光滑重新组合。

基元形式：用基元杂凑演算法将统计数据分到相关联的桶中，未来降低精确度损失，通常采用局部脆弱基元（LSH）演算法，使相似的向量其相关联的基元值也相似。向量定量形式：将向量内部空间中的dealing其中两个有限开集展开代码来获得两个更加保距的向量表观。例如右图将两个128维的向量重新组合成4个32维的向量，将两组32维的统计数据埃唐佩县256类，预测器的每一温大，都用子内部空间的控制点服务中心来近似于，相关联的代码即为类服务中心的ID，每一子内部空间可用8位（2^8=256）表示。

征迁平方根定量

为的是更进一步大力推进搜寻，先将原始统计数据展开埃唐佩县二个（nlists）类，通常埃唐佩县数百类，接着对每一类继续执行向量定量代码。在搜寻时，先依照每一类的服务中心与查阅向量的距取二个（nprob），接着在这nprob个常量中继续执行向量定量搜寻。

可以说是对搜寻内部空间展开了更进一步的拆分，以更进一步增大搜寻覆盖范围。

Faiss常用索引类型

Fasiss架构主要全力支持以下几种向量索引形式

比较重要的参数主要有：

d: 向量维度；nlists: 用于有征迁表的索引，比如IndexIVFPQ，指的是征迁表的数量（控制点的簇数）；quantizer：定量形式，用于有征迁的索引，实际上它指的是征迁表中每一子内部空间的索引类型，可以是IndexFlat*、IndexLSH、IndexPQ或是其他HMPP搜寻索引类型；nbits：向量代码维度，取值只能为8, 12 或是16，并且d是nbits的整数倍；M：向量定量时被重新组合的段数，d必须时M的整数倍；Metric：距测度形式，0表示内积，1表示L2。

Python API采用形式

Faiss的采用主要分两步

构建索引：这部分通常离线完成，也可以HMPP构建也可以增量构建，对于带征迁的索引需要有两个train的步骤。在线查阅：线上服务部分，依照输入的查阅向量返回topK相似的向量。

从文件中读取包含待构建索引的向量

def read_vectors(input_dir, vec_col=0, id_col=-1): if not os.path.exists(input_dir): print("SystemLog: File {} NOT FOUND\n".format(input_dir)) raise FileNotFoundError input_files = os.listdir(input_dir) print("SystemLog: Will read file {} from {}\n".format(input_files, input_dir)) vec_res = []; id_res = [] for file in input_files: file_path = os.path.join(input_dir, file) with open(file_path, r, encoding=utf8) as f: for line in f: line_sep = line.strip().split(SEP) vec_str = line_sep[vec_col] vec = [float(s) for s in vec_str.split(VEC_SEP)] vec_res.append(vec) if id_col>=0: id_res.append(int(line_sep[id_col])) if len(id_res)<1: id_res = None else: id_res = np.array(id_res) return np.array(vec_res).astype(float32), id_res

构建索引

def build_index(data, index_type="IndexIVFPQ", quantizer_type="IndexFlatIP", nlist=1, m=1, nbits=8, dist_metric=0, *args, **kwargs): d = len(data[0]) index = None if index_type == "IndexFlatL2": index = faiss.IndexFlatL2(d) elif index_type == "IndexFlatIP": index = faiss.IndexFlatIP(d) elif index_type == "IndexLSH": index = faiss.IndexLSH(d, nbits) elif index_type == "IndexPQ": index = faiss.IndexPQ(d, m, nbits) if index is not None: index.add(data) return index quantizer = None if quantizer_type == "IndexFlatL2": quantizer = faiss.IndexFlatL2(d) elif quantizer_type == "IndexFlatIP": quantizer = faiss.IndexFlatIP(d) elif quantizer_type == "IndexLSH": quantizer = faiss.IndexLSH(d, nbits) elif quantizer_type == "IndexPQ": quantizer = faiss.IndexPQ(d, m, nbits) metric = faiss.METRIC_INNER_PRODUCT if dist_metric == 1: metric = faiss.METRIC_L2 if index_type == "IndexIVFFlat": index = faiss.IndexIVFFlat(quantizer, d, nlist, metric) elif index_type == "IndexIVFPQ": index = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8) index.train(data) index.add(data) return index

继续执行批量搜寻

def batch_query(query_arr, index, k=1, nprobe = 1, ids=None): index.nprobe = nprobe _, I = index.search(query_arr, k) if ids is not None: I = ids[I] return I

例如

import numpy as np d = 64 # dimension nb = 100000 # database size nq = 10000 # nb of queries np.random.seed(1234) # make reproducible xb = np.random.random((nb, d)).astype(float32) xb[:, 0] += np.arange(nb) / 1000. xq = np.random.random((nq, d)).astype(float32) xq[:, 0] += np.arange(nq) / 1000. index = build_index(data=xb, iindex_type="IndexIVFPQ", quantizer_type="IndexFlatIP", nlist=1, m=1, nbits=8, dist_metric=0) res_ids = batch_query(xq, index, topk=5, nprobe=1) print(res_ids)